Geometría Fractal, Introducción
La geometría fractal está compuesta por formas geométricas complejas: llamadas fractales, que se encuentran principalmente en la naturaleza: cómo en la forma de los árboles, hojas, rocas, etc.
La principal característica de un fractal es la autosemejanza: al analizar un estructura geométrica fractal, vemos cómo hay una forma geométrica básica que se repite hasta el infinito, dicha forma se denomina semilla.
Para la construcción de un fractal, siempre, partiremos siempre de un patrón semilla, al que se aplican unas transformaciones definidas. De modo que esa forma inicial se va fragmentando en más formas, la aplicación de estas transformaciones se denomina iteración. Contra más iteraciones se apliquen a la semilla se conseguirá un fractal más perfecto. Si llegáramos a infinitas iteraciones, entonces estaríamos hablando de un fractal totalmente perfecto y completamente fragmentado.
Elección de la semilla, Demostración
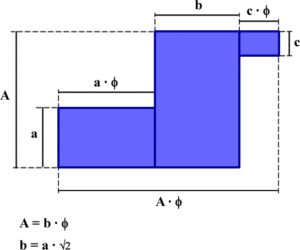
Se ha partido de la premisa que la semilla debe estar contenida dentro de un rectángulo y no debe ser muy simétrica. La semilla propuesta no presenta ninguna simetría. Está compuesta por tres rectángulos de proporción f con una peculiaridad:
- La altura de uno de los rectángulos con la base de otro de los rectángulos guarda una proporción raíz de 2.
A continuación se muestra una imagen con las proporciones que se deberán mantener en cada nueva iteración, para generar el fractal.
Demostración
A continuación se muestra una aplicación práctica de la construcción del fractal según la semilla anteriormente especificada: